無限に続く数を有限の数に近似してまるめると＝１.41421356・・・　近似式として　99/70

１．　無理数を連分数に表して、分母、分子を2桁で近似すると

 

 

 

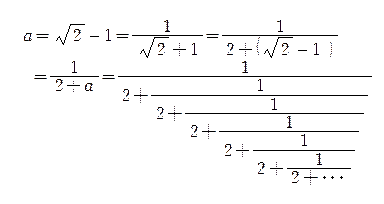
はの小数部分である。

 

 

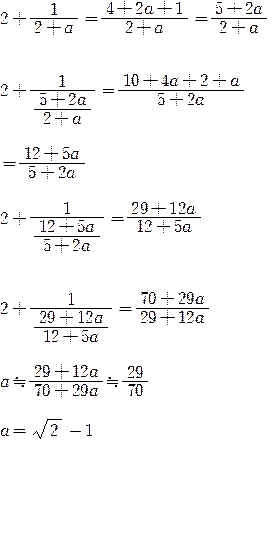
はの小数部分であるので、上式の分母、分子の第2項を第1項に比べて小さいので無視すると

 

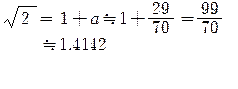
とあらわせます。

 

２.   　古代ギリシャ時代での、開平の方法（高校数学Ⅰ課題学習より）

　正の数Aについて、A=とおくと、（を小さくとる）

　A＝において、は非常に小さいので無視すると

　

　　となる。このとき、は、よりもに近い。

　

　　　　＝

　　　　　　＝　　　　　　　　　　　　①

①    式を利用してを求めると　（A=2　　a＝1　とおく）

 

　

次に同じ操作を繰り返すと　（a＝　A=2 とおく）

　

　＝＝

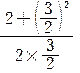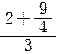次に同じ操作を繰り返すと　（a＝　A=2 とおく）

 

　＝＝

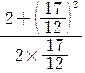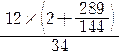　　　＝＝＝＝1.41421569

 

２.       有理数・無理数の連分数表示は(ref.知の追及講座（http://www.kawaijuku.ac.jp/report/kazunokao）より).

 

　例えば.を考える。

　　　. ＝3+　　整数部分（3）+小数部分（）に分ける。

　　以後、小数部分に注目して、小数部分の逆数（1より大）をとり、同じ操作を繰り返していきます。

 

　　　　＝1+　　　　

 

　　　　＝4+0　　(小数部分は0となり、この逆数を取り整数部分と小数部分に分ける操作はここで終わりになります。

 

 

以上の2回の操作を式に表すと

 

　　　　＝3+＝3+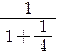

 

実数＝整数部分+小数部分に分け。小数部分の逆数をとり、これを、また、整数部分と小数部分に分ける操作をくりかえ　　　　　　　　　　　　していきます。

 

　　実数＝整数部分+小数部分＝整数部分+＝整数部分+

 

 

　　＝1.414・・・＝1+（-1）　　　（-1）が小数部分なのでこの逆数をとると

 

　　　　＝＝+1

　これを整数部分と小数部分に分けると

 

　　+1＝2+（-1）

となり、同じ小数部分が出てきます。整数部分が2なので

 

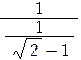　　　＝1+（-1）＝1+　＝1+　＝1+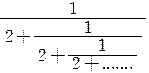　

 

 

３.     黄金比と連分数

 

　　＝1+　　＝1+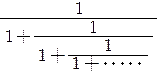　

 

この連分数は

　

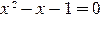
　このは　　であり、＞1　or　＞0より

 

　＝1.61803398・・・（黄金数、黄金比）